基本信息
- 项目名称:
- 人群高流动情形下传染病传播过程的模拟仿真及防控策略研究
- 来源:
- 第十二届“挑战杯”省赛作品
- 小类:
- 生命科学
- 大类:
- 自然科学类学术论文
- 简介:
- 本文以经典的SIR模型为基础,建立传染病动力学模型,通过计算机模拟重现了传染病传播过程。研究发现,对于传染性不是很强的情形,适当地提高人群流动性相当于及时进行了感染人群疏散,有利于避免传染病的快速传播。因此,通过针对特定传染病的模拟我们可以计算得出在哪一个区间才是真正合适的免疫接种的范围,以此来抑制传染病的大爆发以及有效地控制传染病的传染程度。
- 详细介绍:
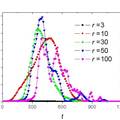
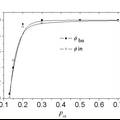
- 人群的高流动性是新世纪以来SARS及H1N1病毒全球肆虐的关键性因素。本文以经典的SIR模型为基础,建立传染病动力学模型,通过计算机模拟重现了传染病传播过程。研究发现,对于传染性不是很强的情形,适当地提高人群流动性相当于及时进行了感染人群疏散,有利于避免传染病的快速传播。首次发现,合适的人群流动性情形下,其感染人群数目呈双峰分布,也即相同感染能力的传染病既有可能导致小爆发,也有可能导致大爆发;深入的研究表明,大爆发的关键成因是感染者无穷大传播网络的形成。而免疫接种的防控效果研究也发现,必须有足够量的接种数目才能有效破坏具有传染能力的无穷大传播网络的形成;过少的接种基本不能防止传染病的爆发,只是在浪费成本;免疫数量存在一个阈值,更多的免疫接种提高了经济成本,却不能以线性效率抑制感染的发生;在某种程度上具有物理相变的双态转变特征。因此,通过针对特定传染病的模拟我们可以计算得出在哪一个区间才是真正合适的免疫接种的范围,以此来抑制传染病的大爆发以及有效地控制传染病的传染程度。 本研究基于经典的SIR模型,用Monte Carlo模拟方法重现传染病跨区域全局性传播的行为特点。SIR模型是Kermack[11] 等人在1927年提出的一个传染病的模型,这个模型得到了历史上发生过的大规模的传染病(如上世纪初在印度孟买发生的瘟疫)数据的有力支持,后来很多研究人员对SIR模型做了推广。 首先假定某地区的人群是一个常数,把他们分为三个部分:易感人群、被感染者、恢复者。易感人群很容易被感染而且还没被感染(Susceptible),用S(t)表示;被感染者是已经被感染而且又将感染其他人(Infected),用I(t)表示;恢复者是他们从流行病中获得免疫并恢复为健康的人(Recovered),用R(t)表示。 我们用一个二维的格子空间(a×a)去模拟人群,用周期边界性条件去模拟一个无限的空间。在此模型当中,人群根据人群密度被随机分布到整个格子空间中,以建立一个均匀的人群分布。在模型中产生的每一个人在某一时刻或某一天都有一个的运动范围,我们用运动半径去描述。例如它可以在最大的运动半径范围内跳跃到其他地方(如图1),而每一个人身边都有四个与自己最邻近的人,只有最相邻的两个人才能发生接触。感染者可以感染易感人群,而同时自己也因为有pr的存在会有可能康复。 当模型初始化的时候,即t=0的时候,有N个感染者自动在模型中生成,而剩下的则是由随机产生的易感人群组成。每次模拟我们都会进行m次,并且我们设定只要感染人群大于Nc,即可认为此次传染病属于一个会爆发的传染病。 本文是基于SIR模型及累积感染基础上使用Monte Carlo模拟方法对传染病传播过程进行了初步模拟。研究发现,对于传染性不是很强的情形,适当的提高人群流动性反而会有利于避免传染病的快速传播,相当于及时进行了密集人群的疏散。研究首次发现,某种情形下,相同感染能力的传染病既有可能导致小爆发,也有可能导致大爆发,其感染人群数目呈双峰分布,也即看似已经灭绝时,如果不继续进行有效的免疫控制,它很可能会在某一时刻以迅雷不及掩耳之势再来一次大爆发,让群众或者相关部门始料未及。对于个体接种的模拟发现,从经济的角度出发,对于免疫接种的数量也要准确把握,免疫数量存在一个阈值,过少的免疫接种无法抑制传染病的肆虐,而过多的免疫接种却会提高治疗的成本。因此,通过模拟我们可以计算得出在哪一个区间才是真正合适的免疫接种的范围,以此来抑制传染病的大爆发以及有效地控制传染病的传染程度。
作品专业信息
撰写目的和基本思路
- 基于计算机模拟方法,重点研究人群流动性对传染病传播动力学的影响。 1.建立特定情形下的传染病传播模型,在此基础上通过计算机模拟重现传染病过程; 2.基于个体的出差概率及活动半径对人群流动性进行物理性描述; 3.模拟研究人群流动性与传染病爆发概率、影响范围之间的关系; 4. 对个体进行随机免疫,研究不同免疫概率情形下传染病的防治效果,进而提出恰当的防控策略。
科学性、先进性及独特之处
- 1. 不同于已有的基于点源扩散模式的流行病传播理论,重点关注了新时代人群流动性对其传播速度、感染范围的影响; 2. 不同于已有数学模型及元胞自动机方法,本研究使用的格子蒙特卡洛模拟方法能够有效重现传染病跨区域性传播这一特点。
应用价值和现实意义
- 广东省是一个人口流动性大省,不但和国内其他地区有着密切的人口对流,而且和香港及境外区域国家有着频繁的人员来往。本研究通过计算机模拟重现人群高流动情形下传染病的传播过程,为相关部门提出针对性防控措施的意见,以避免更多的传染病大爆发。
学术论文摘要
- 人群的高流动性是新世纪以来SARS及H1N1病毒全球肆虐的关键性因素。本文以SIR模型和累积感染为基础,建立传染病动力学模型,通过计算机模拟重现了传染病传播过程。研究发现,对于传染性不是很强的情形,适当的提高人群流动性相当于及时进行了感染人群疏散,有利于避免传染病的快速传播。首次发现,某种情形下,其感染人群数目呈双峰分布,也即相同感染能力的传染病既有可能导致小爆发,也有可能导致大爆发;深入的研究说明,大爆发的关键成因是传播网络的形成。而免疫接种的防控效果研究也发现,必须有足够量的接种数目才能有效破坏传播网络的形成;过少的接种基本不能阻止传染病的爆发,只是在浪费成本;免疫数量存在一个阈值,过多的免疫接种并不能进一步有效抑制感染的发生,却会大大提高经济成本。因此,通过针对特定传染病的模拟我们可以计算得出在哪一个区间才是真正合适的免疫接种的范围,以此来抑制传染病的大爆发以及有效地控制传染病的感染程度。
获奖情况
- 暂无
鉴定结果
- 暂无
参考文献
- [1] M.J Keeling, and P.Rohani. Modeling Infectious Diseases in Humans and Animals, Princeton, N.J.: Princeton University Press(2007) [2] Z.MA,Y.Zhou, and J.Wu.Modeling and Dynamics of Infectious Diseases World Scientific Publishing Company(2009). [3] X.N. Han, S.J. de Vlas,L.Q.Fang,D. Feng, W.C. Cao.Mathematical modeling of SARS and other infectious disease in China:a review. Tropical Medicine & International Health,14:92-100(2009) [4] J.Li, and X.F.Zou. Modeling Spatial Spread of Infectious Diseases with a Fixed Latent Period in a Spatially Continuous Domain. Bulletin of Mathematical Biology,71(8): 2048-2079(2009) [5] 许田,张培培。姜玉梅,苏蓓蓓,何大韧.流行病传播模型与SARS.自然杂志,26(1):20-25(2004) [6] 石耀霖.SARS传染扩散的动力学随机模型.科学通报,48(13):147-152(2004) [7] 余雷,薛惠锋,李刚:传染病传播模型研究,计算机仿真,2007年,第24卷,04期 [8] B .Dybiec. Modelling control of epidemics spreading by long-range interactions. Journal of Royal Society Interface,6(39):941-950(2009)
同类课题研究水平概述
- 不同于其他的科学研究,对传染病的研究一般不能采取实验方式,主要有如下三种研究手段:描述性研究、理论性研究及模拟仿真研究。 描述性研究主要是针对各类传染病的数据资料,使用已有的数学函数行进数值拟合,进而对传染病过程及感染力度等进行相信分析描述;这种方法基于大量数据资料,分析客观真实,具有很高的参考价值,但同时也是一种比较唯象的研究方法,不能揭示传染病的传播机制及空间分布情况。 理论性研究则首先建立确定的数学模型,通过建立各类个体(易感者、感染者、免疫者)数量随时间动态变化的微分方程或偏微分来描述其传播过程和机制;其中最有影响的是SIR和SIS模型,前者可以有效描述麻疹流行病。而后者可以有效描述肺结核和淋病等流行病。比较遗憾的是,现有的微分方程模型只能描述感染个体数量随时间的变化过程,不能描述传染病传播的空间变化趋势。近期也有学者做了不少尝试,比如基于中心地理考虑了个体全球流动对SARS传播的影响,或在数学模型中引入了反应扩散动力方程以便考虑空间因素。 近年来,得益于计算机计算能力及模拟仿真的技术的快速发展,元胞自动机模拟、人工神经网络模拟、随即动力学模拟被成功地用来模拟传染病在空间上的传播过程。尤其是随机动力学模拟方法被越来越多的使用,因为后者可以容易使人群在空间流动。国内外一些同行也已经注意到了传染病跨区域的空间“飞点”传播特点,并利用遥感学方法或随机动力学模拟方法进行了简单探讨,但是还没有展开系统的研究,对其物理图像仍然缺乏清晰的认识,更谈不上对于此类传染病防控策略的探究。