基本信息
- 项目名称:
- 分数阶混沌系统的同步与控制
- 来源:
- 第十二届“挑战杯”作品
- 小类:
- 机械与控制
- 大类:
- 自然科学类学术论文
- 简介:
- 项目针对混沌系统尤其是分数阶系统实现其有效的控制与同步,为其在保密通信的应用和其他复杂系统的控制提供理论依据。我们提出了新的混沌系统,并对其进行了详尽的复杂动力学特征分析,同时实现了系统的同步,对混沌系统实现了线性反馈和自适应控制,并对两方法进行了比较分析,提出了一类参数不确定的分数阶系统在有扰动情况下的滑模变结构控制,并给出了理论分析和数值模拟仿真分析。
- 详细介绍:
- 项目对混沌系统尤其是分数阶系统实现其有效的控制与同步,为其在保密通信的应用和其他复杂系统的控制提供理论依据,并提出了一类参数不确定的分数阶系统在有扰动的情况下的滑模变结构控制,并实现了数值模拟仿真。我们在《The Recursive Inversion of Nonlinear Control of a Four-dimensional Hyperchaotic System》(IEEE,EI) 中针对四维的超混沌系统提出了一种新的递归反推控制方法。在《只含一个非线性项的超混沌系统及其电路实现》中提出了 一个 新的只含一个非线性项的混沌系统,并对其进行了详尽的复杂动力学特征分析,同时实现了系统的电路仿真。项目在《Control of a class of fractional-order chaotic systems via sliding mode》(SCI)中针对一类分数阶混沌系统应用滑模变结构控制法成功的实现了一类分数阶系统的控制,并在分数阶的Chen系统和Lorenz等系统得到验证,经过仿真验证该方法能够有效迅速的将分数阶混沌系统镇定在固定点和周期轨道上。我们在文章《只含一个非线性项的超混沌系统及其控制比较》中对混沌系统应用线性反馈和自适应控制实现了对系统的控制,并对两方法进行了比较分析。 我们项目的实际应用领域包括1、保密通信领域; 2、复杂系统的建模与控制。
作品专业信息
撰写目的和基本思路
- 对混沌系统尤其是分数阶系统实现其有效的控制与同步,为其在保密通信的应用和其他复杂系统的控制提供理论依据。
科学性、先进性及独特之处
- 提出了新的只含一个非线性项的混沌系统,并对其进行了详尽的复杂动力学特征分析,同时实现了系统的同步,对混沌系统实现了线性反馈和自适应控制,并对两方法进行了比较分析,提出了一类参数不确定的分数阶系统在有扰动的情况下的滑模变结构控制,并实现了数值模拟仿真。
应用价值和现实意义
- 1、保密通信领域; 2、复杂系统的建模与控制。
学术论文摘要
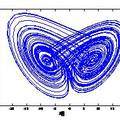
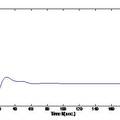
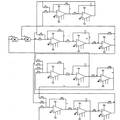
- 我们在讨论分数阶混沌系统时构造出了一个新的只含有一个非线性项的四维非线性动力学系统, 研究了该系统的超混沌吸引子Lapunov指数、庞加莱映射图等复杂动力学特征, 然后以Multisim电路仿真软件为平台进行了仿真实验,为了更好控制此四维超混沌系统,分别用线性反馈控制法和自适应控制法对该超混沌系统进行了控制仿真,同时比较了两种控制方法控制混沌系统的优缺点。最后,本研究提出了一类参数不确定的分数阶混沌系统的滑模变结构控制方法,分别就有无噪声扰动的两种情况,并通过理论分析和数值仿真验证。
获奖情况
- 1. 陈海涛, 陈帝伊, 申滔, 马孝义. 只含一个非线性项的超混沌系统及其电路实现[J]. 微型机与应用, 2010, 14: 85-88 2. Chen Hai-Tao, Chen Di-Yi, Ma Xiao-Yi. The recursive inversion of nonlinear control of a four-dimensional hyperchaotic system[J]. 2010 IEEE International Conference on Intelligent Computing and Integrated Systems, ICISS2010, Guilin China October 22-24, 2010. 3. Chen Di-Yi, Liu Yu-Xiao, Ma Xiao-Yi, Zhang Run-Fan. Control of a class of fractional-order chaotic systems via sliding mode [J]. Nonlinear Dynamics, 2011, DOI: 10.1007/s11071-011-0002-x (SCI源刊) 4. 陈帝伊, 陈海涛, 马孝义, 龙燕. 只含一个非线性项的超混沌系统及其控制比较[J]. 计算机应用, 2010, 30(8): 2045-2048.
鉴定结果
- 项目有SCI一篇、EI一篇国内核心两篇
参考文献
- 1. 陈向荣,刘崇新,李永勋.基于非线性观测器的一类分数阶混沌系统完全状态投影同步 [J]. 物理学报,2008,57(3):1453-1457. 2. 吴峥茂. 非线性混沌系统分析和控制问题的研究 [D]. 上海交通大学.2007. 3. 胡建兵. 分数阶混沌稳定性理论及同步方法研究 [D]. 中北大学.2008. 4. S.H. Hosseinnia,R. Ghaderi,A. Ranjbar N.Sliding mode synchronization of an uncertain fractional order chaotic system[J].Computers and Mathematics with Applications 59 (2010) 1637-1643.
同类课题研究水平概述
- 分数阶的微分方程早在17世纪就被提出,但是直到近年来才引起学术界的关注且被广泛应用于工程上。已知的很多系统都是分数阶的,例如电解质和电介质的极化作用、雷达信号、粘滞系统等。很多分数阶系统表现出混沌现象,比如分数阶的Chen系统、Duffing系统以及Lorenz系统等。 最近研究成果表明分数阶混沌系统是可以控制与同步的。在分数阶混沌系统的控制与同步方面,主要包括线性反馈法、非线性反馈法、滑模变结构法以及基于Lyapunov方程的Backstepping控制方法。在研究分数阶混沌系统方面的主要成果有王兴元等(大连理工大学)分数阶统一混沌系统的投影同步(物理学报)中改变系统参数计算了分数阶统一系统的最大Lyapunov指数和关联维数,研究了分数阶统一系统的动力学行为,并实现了分数阶统一混沌系统的投影同步。西安交通大学的刘崇新等基于波特图的频域近似方法,提出了一种混合型电路单元来近似实现分数阶算子,并设计相应的控制器,实现了对分数阶系混沌系统的控制。上海交通大学吴峥茂在其博士论文中针对分数阶系统混沌参数域的问题,利用在整数阶非线性系统中应用成功的谐波平衡原则分析了分数阶非线性系统的混沌参数域问题。通过具体分析分数阶动态系统Genesio.Tesi的参数域实例得到很多分数阶系统区别于整数阶系统的结论。 Sara Dadras在Control of a fractional-order economical system via sliding mode中应用滑模变结构法控制了分数阶的金融系统并证明了滑模变结构法控制系统具有很强的鲁棒性。Varsha Daftardar-Gejji发表了Chaos in fractional ordered Liu system,在这篇文章中Varsha Daftardar-Gejji详细的分析了Liu系统的分数阶混沌现象并且得出了Liu系统在对称条件下出现混沌的最低阶数为2.76,对称条件下为2.60。 S.H. Hosseinnia等在他们的文章Sliding mode synchronization of an uncertain fractional order chaotic system中以参数不定的 Duffing_Holmes系统为例,利用滑模变结构法成功的控制了该系统。