基本信息
- 项目名称:
- 广义Camassa-Holm方程的显式周期波解及其分支
- 来源:
- 第十二届“挑战杯”作品
- 小类:
- 数理
- 大类:
- 自然科学类学术论文
- 简介:
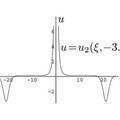
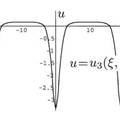
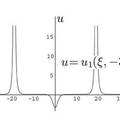
- 根据大量计算机模拟提供的信息和动力系统分支理论,我们推导了广义 Camassa—Holm 方程的光滑周期波和周期爆破波的显式表达式,证明了光滑周期波能演化成光滑孤立波,周期爆破波能演化成单爆破波。特别的,我们发现周期爆破波也能演化成光滑孤立波,别的方程从来没有见过这种现象。我们的工作为该现实模型提供了理论依据和控制方法,我们的主要结果发表在SCI收录杂志IJBC上,已经被SCI检索。
- 详细介绍:
- 根据大量计算机模拟提供的特殊的周期轨道的特点,结合动力系统,行波系统的分支理论,我们推导了广义 Camassa—Holm 方程的光滑周期波和周期爆破波的显式表达式,不仅找到了分支变化临界点,也证明了光滑周期波能演化成光滑孤立波,周期爆破波能演化成单爆破波。 更值得一提的是,我们发现周期爆破波也能演化成光滑孤立波,这是一种新的非线性现象,在别的方程从来没有见过这种现象。结合已有结论,我们的结果从一个侧面刻画了非线性偏微分方程的积分流形的分类。 我们的工作为该方程所代表的实际模型的应用提供了理论依据和参数选取范围,我们的主要结果发表在SCI三区杂志IJBC上,已经被SCI检索。
作品专业信息
撰写目的和基本思路
- 目 的:研究广义Camassa-Holm方程的显式周期波解的存在性及分支情况。 基本思路:首先通过计算机对该方程的行波系统作模拟实验,找出周期轨并观察其变化情况,然后根据实验提供的信息,从理论上证明特殊周期轨的存在条件及变化趋势,最后利用特殊周期轨的表达式来导出原方程的显式周期波解及其分支情况。
科学性、先进性及独特之处
- 首先我们的结果包含了以前文献的许多结论,对以前的结论做了推广(我们不限制方程的解的波速,不要求方程系数确定)。 其次我们发现了新的分支现象,即从周期爆破解能分支出光滑孤立波解。结合前人已经有的结果,我们的工作从一个侧面反映了非线性偏微分方程的积分流形的分类问题上的一个更深刻的结果。 最后我们给出了确定的分支变化的临界值,这对实际应用提供了理论支持和参数范围。
应用价值和现实意义
- 首先为研究高次的非线性数学物理方程的显式周期波解提供了一种方法; 其次为该方程所代表的实际模型的分析提供了参数范围和理论依据; 从数学上,我们的工作是前人在孤立波的分支问题上的工作的推广。
学术论文摘要
- 本文研究广义Camassa-Holm方程的显式周期波解及其分支,首先通过计算机对该方程的行波系统作了大量的数值实验,然后根据实验提供的信息,从理论上推导出了分支参数值为k以及分支波速值为c1和c2,对于c1与c2之间的波速c,还推导出了初始位置的4个分支值a1,a2,a3及a4,最后,利用行波系统的一些特殊周期轨道,导出了以上方程的显式周期波解,并讨论了这些周期波解的分支情况,特别地,我们发现了一个新分支现象,即由一个周期爆破解能分支出一个光滑孤立波解,其结果改进和推广了前人的一些工作。
获奖情况
- (1)本文的主要结果发表在SCI杂志:I. J. Bifur. & Choas (2010) Vol. 20,No.8, 2507—2519. 已被SCI收录。 (2)本参赛作品获得2011年5月校内挑战杯赛的特等奖。 (2)本参赛作品获得2011年5月本省挑战杯赛自然科学论文数理类的特等奖。
鉴定结果
- 主要结果发表在SCI杂志:I. J. Bifur. & Choas(2010)Vol. 20,No.8, 2507—2519. 可以检索到DOI:10.1142/S0218127410027131
参考文献
- 利用数学软件Mathematica能检验本文结果的正确性。
同类课题研究水平概述
- 研究数学物理方程的解和对解的分析一直是数学物理学家们的一个重要研究领域,我所研究的方程是流体力学中的一个数学模型,很多学者都对该方程进行过研究: [1] Liu, Z. R. & Qian, T. F. [2001] “Peakons and their bifurcation in a generalized Camassa–Holm equation,” Int. J. Bifurcation and Chaos 11, 781–792. [2] Liu, Z. R. & Ouyang, Z. Y. [2007b] “A note on solitary waves for modified forms of Camassa–Holm and Degasperis–Procesi equations,” Phys. Lett. A 366, 377–381. [3] Liu, Z. R. & Guo, B. L. [2008] “Periodic blow-up solutions and their limit forms for the generalized Camassa–Holm equation,” Prog. Natural Sci. 18, 259–266. [4] Liu, Z. R. & Pan, J. [2009] “Coexistence of multifarious explicit nonlinear wave solutions for modified forms of Camassa–Holm and Degaperis–Procesi equations,” Int. J. Bifurcation and Chaos 19, 2267–2282. [5] Shen, J. W. & Xu, W. [2005] “Bifurcations of smooth and non-smooth travelling wave solutions in the generalized Camassa–Holm equation,” Chaos Solit. Fract. 26, 1149–1162.等。 以上作者主要针对固定的参数研究(固定的行波速或方程的系数),因此我们的结果包含了以上文献中的许多结果。