基本信息
- 项目名称:
- 基于混合遗传算法的矩形件优化排样系统
- 来源:
- 第十二届“挑战杯”省赛作品
- 小类:
- 信息技术
- 大类:
- 科技发明制作A类
- 简介:
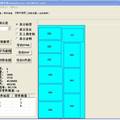
- 本系统是基于遗传算法、剩余矩形匹配分割算法和最低水平线择优插入算法而设计的一个大规模板材优化排样系统,可以提高板材的利用率,降低产品成本。本系统可将排样结果导出为HTML格式、G代码格式和CAD格式,并可将排样结果图直接通过打印机打印出来,从而可以满足工业上的不同要求。
- 详细介绍:
- 大规模矩形件优化排样是一个典型的组合优化问题,属于NP-hard问题,至今也没有一种多项式时间算法。本系统首先将最低水平线择优插入算法的局部搜索和遗传算法的全局搜索相结合,实现了矩形件的优化排样。然而,在实际工程中,对一个排样方案中的矩形件进行切割时,经常会提出满足“一刀切”的下料工艺要求。“一刀切”的要求实际上增加了排样的约束条件。因此,本文又设计了矩形匹配分割算法和遗传算法相结合的排样算法,从而满足“一刀切”的工艺要求。最后,基于以上理论,用C++实现了矩形件优化排样系统,本系统可将排样结果导出为HTML格式、G代码格式和CAD格式,从而可以满足工业上的不同要求。实验结果表明,本系统能给出很好的矩形件排样的优化方案,可以显著提高板材的利用率。
作品专业信息
设计、发明的目的和基本思路、创新点、技术关键和主要技术指标
- 与已有技术相比,本系统具有以下特点:本系统结合了剩余矩形匹配分割算法和最低水平线择优插入算法的局部搜索性能和遗传算法的全局搜索性能,可以更有效地解决大规模多规格的板材和矩形件的排样优化问题。计算实例表明本系统可以找到比较好的排样方案。由于本系统可以实现板材的“一刀切”要求,并考虑了下料工艺中的切缝宽度问题,因此本系统不仅可以应用于不同规格板材的套排,还可用于单块板材及卷材,具有更好的适用性和实用性。本系统还可以将排样结果以HTML、CAD和G代码等各种文件形式导出,可以满足不同的工业要求。
科学性、先进性
- 本系统是基于遗传算法、剩余矩形匹配分割算法和最低水平线择优插入算法而设计的一个大规模板材优化排样系统,可以提高板材的利用率,降低产品成本。实验结果表明,本系统能给出很好的矩形件排样的优化方案,可以显著提高板材的利用率。
获奖情况及鉴定结果
- 2011年1月本作品获得大连市第二届大学生创新创意作品大赛一等奖; 2011年3月宁波路径有限公司购买了本系统。
作品所处阶段
- 软件成品。
技术转让方式
- 软件。
作品可展示的形式
- 软件。
使用说明,技术特点和优势,适应范围,推广前景的技术性说明,市场分析,经济效益预测
- 本系统可在Windows XP等操作系统上运行。本系统是基于遗传算法、剩余矩形匹配分割算法和最低水平线择优插入算法而设计的一个大规模板材优化排样系统,可以提高板材的利用率,降低产品成本。实验结果表明,本系统能给出很好的矩形件排样的优化方案,可以显著提高板材的利用率。本系统适用于冲裁件排样、造船、车辆、家具生产、玻璃切割等工业领域。本系统是一个较完善的矩形件排样系统,将智能算法和运筹学算法相结合,适用于工业的板材切割,具有广阔的市场前景。
同类课题研究水平概述
- 国外有关下料排样问题的研究起步比较早。最早关于排样的文章是前苏联人Kantovorich 在 1939 年发表的,讨论一维下料问题。五十年代中期,Paull, Eisemann,Herrmann 和 Vajda率先提出用线性规划(Linear Programming)方法解决印刷和造纸工业的矩形件排样问题,但材料利用率不高。Garey 和 Johnson证明用数学规划(Mathematical Programming techniques)的方法解决二维切割问题是优化问题中具有最高计算复杂度的一类优化计算问题——NP 完全问题。60 年代初,Gilmore 和 Gomory发表了四篇著名的文章,提出了一维下料方案和二维排样问题。70 年代至今,许多学者对排样问题进行了大量的研究,取得了一定的成果。但排样问题为 NP 完全问题,复杂难解;同时由于排样时存在各种限制条件,因此至今也没用通用的标准方法来进行求解。由于排样问题的复杂性和广泛性,在 1988 年的 Paris EURO/TIMS 国际会议上,专门成立了下料问题兴趣小组 ESICUP(EURO Special Interest Group on Cutting and Packing Problem)。 由于研究矩形件排样既可以直接解决矩形件排样问题,也可以作为解决二维不规则零件排样问题的基础,所以一直是众多学者研究的热点,有大量的研究成果出现。