基本信息
- 项目名称:
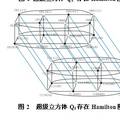
- 超级立方体Qn的hamilton圈研究
- 来源:
- 第十二届“挑战杯”省赛作品
- 小类:
- 信息技术
- 大类:
- 自然科学类学术论文
- 简介:
- 本作品利用图的笛卡尔积的概念来定义超级立方体Qn,讨论图的同构与图的笛卡尔积之间的关系,证明Qn中存在Hamilton圈,给出Qn中Hamilton圈的生成算法,从理论和实践上解决了Qn中Hamilton圈问题。
- 详细介绍:
- 给定一个图G,我们并不是直接讨论它的Hamilton圈的存在性,而是讨论笛卡尔积H=GK2的Hamilton圈的存在问题,如果图G存在Hamilton圈,那么GK2也存在Hamilton圈,这样使得我们可以把一些特殊的图分解成某一个图G和K2的笛卡尔积,从而由G的Hamilton性来得出特殊图的Hamilton。 多处理器网络是由图的笛卡尔积构造的,如网格,超立方体等。积网络组成了非常重要的一类互联网产品的网络构成了非常重要的类互连网络[1]。无向图中Hamilton圈是遍历图中每个顶点恰好一次又返回起点的圈。确定一个图中这样的圈是否存在就是Hamilton圈问题,它是一个NP完全问题。实际应用(特别是计算机网络中的应用)和计算复杂性的研究推动了Hamilton圈问题的研究[1][2][3][4]。Hamilton圈问题的研究由来已久。Dirac于1952就证明了:如果G是至少有三个顶点的简单图且每个顶点的度数大于等于n/2存在Hamilton圈; Bondy-Chvátal1972年给出了定理:一个图存在Hamilton圈的充要条件是它的闭包存在Hamilton圈;Tutte也于1956年证明每一个4-连通的平面图存在Hamilton圈[5]。宋玉梅在1999年证明:一个简单图存在Hamilton圈的充要条件是其PerGR非零[6]。与此同时,对一些特殊图的Hamilton圈问题的研究也很活跃。例如,Fleischner研究了图的平方中Hamilton圈问题,并于1974年证明了:如果G是一个2-连通的图,那么G2存在Hamilton圈[5];Chvátal于1985年研究了旅行商问题中Hamilton圈[7];Jackson1980年证明了度数至少为n (G) / 3的任意简单正则图存在Hamilton圈[8], 这一结论由Zhu Y. J., Z. H. Liu和 Z. G. Yu等人进行了改进[9]。本文研究超立方体网络中的Hamilton圈。
作品专业信息
撰写目的和基本思路
- 本作品利用图的笛卡尔积的概念来定义超级立方体Qn,讨论图的同构与图的笛卡尔积之间的关系, 证明Qn中存在Hamilton圈,给出Qn中Hamilton圈的生成算法,从理论和实践上解决了Qn中Hamilton圈问题。
科学性、先进性及独特之处
- 超级立方体是纳米计算机的基本结构,作为多核计算机技术的中间体系结构,研究超级立方体Qn的性质无疑具有重要意义。本作品从理论上证明了Qn中存在Hamilton圈,揭示了Qn中Hamilton圈的生成过程,全面系统讨论了图的笛卡尔积和图的同构的关系,为寻找图中的Hamilton圈问题开辟了新的方法和思路。
应用价值和现实意义
- 本作品系统地运用图理论分析了图的笛卡尔积和图的同构的关系, 对Qn中的Hamilton圈问题, 既有理论证明, 又有具体的生成算法, 彻底解决了Qn中Hamilton圈问题, 将为设计互联网算法提供更好的思路。在容错超立方体网络中,为满足局部连通性条件的超立方体网络中高效的容错路由算法,提供了一种新思路。在超立方体多微处理机系统以及超立方体计算机网络中有很好的应用价值。
学术论文摘要
- 给定一个图G,我们并不是直接讨论它的Hamilton圈的存在性,而是讨论笛卡尔积H=GK2的Hamilton圈的存在问题,如果图G存在Hamilton圈,那么GK2也存在Hamilton圈,这样使得我们可以把一些特殊的图分解成某一个图G和K2的笛卡尔积,从而由G的Hamilton性来得出特殊图的Hamilton。 超立方体是互联网的一种基本类型, 作品利用图的笛卡尔积的概念来定义超立方体Qn, 讨论了图的同构与图的笛卡尔积之间的关系, 证明了超立方Qn (n≥1)中存在Hamilton圈, 给出Qn中Hamilton圈的生成算法, 同时对Qn的其他性质, 如欧拉性和二部性等也进行了介绍。
获奖情况
- 无
鉴定结果
- 无
参考文献
- 参考技术: Lih-Hsing Hsu, Cheng-Kuan Lin写了一本关于图论和互联网的专著, 宋玉梅在1999年证明: 一个简单连通图存在Hamilton圈的充要条件是其邻接矩阵的恒式PerGR非零, Jackson1980年证明了度数至少为n (G) / 3的任意简单正则图存在Hamilton圈,这一结论由Zhu Y.J.,Z.H.Liu和 Z.G.Yu等人进行了改进,王艳芳给出了2npm阶群上Caylay图的Hamilton圈分解, Yan zhong Hu, Hao Li对8阶立方图(3正则图)进行了分类,并证明了它们的hamilton性。 主要参考文献: [1] Lih-Hsing Hsu, Cheng-Kuan Lin, Graph Theory and Intrerconnection Networks, New York: CRC Press, Sept. 2008, pp. 171–221. [2] Gary Chartrand and Ping Zhang(美).范益政, 汪毅, 龚世才, 朱明译.图论导引.北京: 人民邮电出版社, 2007, pp. 122–132. [3] J Douglas B.West(美).李建中, 骆吉州译.图论导引.北京: 机械工业出版社, 2006, pp. 229–231. [4] Bondy, J. A. and Murty, U. S . R. , Graph Theory with Applications, Macmillan Press Ltd. , 1976, pp.3–5. [5] Reinhard Diestel, Graph Theory 3rd ed, Beijing: , Mar. 2008, pp.275–278. [6] 宋玉梅, 关于 Hamilton 图的充分必要条件, 长春大学 学报, Vol.19, No.13, June, 1999, pp. 15-16.
同类课题研究水平概述
- 无向图中Hamilton圈是遍历图中每个顶点恰好一次又返回起点的圈。确定一个图中这样的圈是否存在就是Hamilton圈问题,它是一个NP完全问题。实际应用(特别是计算机网络中的应用)和计算复杂性的研究推动了Hamilton圈问题的研究。 Hamilton圈问题的研究由来已久。 Bondy-Chvátal1972年给出了定理: 一个图存在Hamilton圈的充要条件是它的闭包存在Hamilton圈; Tutte也于1956年证明每一个4-连通的平面图存在Hamilton圈。宋玉梅在1999年证明: 一个简单连通图存在Hamilton圈的充要条件是其邻接矩阵的恒式PerGR非零。与此同时,对一些特殊图的Hamilton圈问题的研究也很活跃。例如, Fleischner研究了图的平方中Hamilton圈问题,并于1974年证明了; 如果G是一个2-连通的图,那么G2存在Hamilton圈; Chvátal于1985年研究了旅行商问题中Hamilton圈; Jackson1980年证明了度数至少为n (G) / 3的任意简单正则图存在Hamilton圈,这一结论由Zhu Y.J., Z.H.Liu和 Z.G.Yu等人进行了改进。 王艳芳2009年给出了2npm阶群上Caylay图的Hamilton圈分解。 2011年,Yan zhong Hu, Hao Li对8阶立方图(3正则图)进行了分类,并证明了它们的Hamilton性。 国内外研究图的Hamilton圈十分活跃,但是关于Qn中Hamilton圈的研究的报告还未见到,作品提到的方法和思想具有创新独特之处,有很好的借鉴作用。